愤怒小鸟 X星球愤怒的小鸟喜欢撞火车!
一根平直的铁轨上两火车间相距 1000 米
愤怒的小鸟从A车出发,时速50米/秒,撞向B车,
问:这期间愤怒的小鸟撞 B 车多少次? 9
注意:需要提交的是一个整数(表示撞B车的次数),不要填写任何其它内容。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 public class Main { public static void main (String[] args) { int times = 0 ; int aSpeed = 10 ; int bSpeed = 10 ; int birdSpeed = 50 ; double currentLength = 1000 ; double spare = 0 ; for (int i = 0 ; currentLength > 1 ; i++) { if ((i & 1 ) == 0 ) { spare = currentLength / (birdSpeed + bSpeed); times++; } else { spare = currentLength / (birdSpeed + aSpeed); } currentLength -= bSpeed * spare + aSpeed * spare; } System.out.println(times); } }
反幻方 我国古籍很早就记载着
2 9 4
这是一个三阶幻方。每行每列以及对角线上的数字相加都相等。
下面考虑一个相反的问题。
比如:
你的任务是搜索所有的三阶反幻方。并统计出一共有多少种。
比如:
7 8 9
2 1 9
等都算作同一种情况。
请提交三阶反幻方一共多少种。 3120
这是一个整数,不要填写任何多余内容。
回溯 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 public class Main { static int [] fang = new int [] { 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 }; static int times = 0 ; public static void main (String[] args) { backTrack(0 ); System.out.println(times / 8 ); } private static void backTrack (int current) { if (current == fang.length - 1 ) { if (isOK()) { times++; } } else { for (int i = current; i < fang.length; i++) { swap(current, i); backTrack(current + 1 ); swap(current, i); } } } private static boolean isOK () { int line1 = fang[0 ] + fang[1 ] + fang[2 ]; int line2 = fang[3 ] + fang[4 ] + fang[5 ]; int line3 = fang[6 ] + fang[7 ] + fang[8 ]; int column1 = fang[0 ] + fang[3 ] + fang[6 ]; int column2 = fang[1 ] + fang[4 ] + fang[7 ]; int column3 = fang[2 ] + fang[5 ] + fang[8 ]; int a = fang[0 ] + fang[4 ] + fang[8 ]; int b = fang[2 ] + fang[4 ] + fang[6 ]; if (line1 == line2 || line1 == line3 || line2 == line3 || line1 == column1 || line1 == column2 || line1 == column3 || line2 == column1 || line2 == column2 || line2 == column3 || line3 == column1 || line3 == column2 || line3 == column3 || line1 == a || line1 == b || line2 == a || line2 == b || line3 == a || line3 == b || a == b || column1 == column2 || column2 == column3 || column1 == column3 || column1 == a || column2 == a || column3 == a || column1 == b || column2 == b || column3 == b) { return false ; } return true ; } private static void swap (int i, int j) { int tmp = fang[i]; fang[i] = fang[j]; fang[j] = tmp; } private static void outPut () { for (int i = 0 ; i < fang.length; i++) { out.printf("%d " , fang[i]); if (i == 2 || i == 5 || i == 8 ) { System.out.println(); } if (i == 8 ) { System.out.println(); } } } }
打靶 小明参加X星球的打靶比赛。
这局小明共打了6发子弹,没有脱靶。
不同环数得分是这样设置的:
那么小明的6发子弹得分都是多少呢?有哪些可能情况呢?
下面的程序解决了这个问题。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 public class Main { static void f (int [] ta, int [] da, int k, int ho, int bu, int sc) { if (ho < 0 || bu < 0 || sc < 0 ) return ; if (k == ta.length) { if (ho > 0 || bu > 0 || sc > 0 ) return ; for (int i = 0 ; i < da.length; i++) { for (int j = 0 ; j < da[i]; j++) System.out.print(ta[i] + " " ); } System.out.println(); return ; } for (int i = 0 ; i <= bu; i++) { da[k] = i; f(ta, da, k + 1 , ho - da[k] / Math.max(da[k], 1 ), bu - i, sc - ta[k] * i); } da[k] = 0 ; } public static void main (String[] args) { int [] ta = { 1 , 2 , 3 , 5 , 10 , 20 , 25 , 50 }; int [] da = new int [8 ]; f(ta, da, 0 , 3 , 6 , 96 ); } }
路径之谜 小明冒充X星球的骑士,进入了一个奇怪的城堡。
假设城堡地面是 n x n 个方格。
按习俗,骑士要从西北角走到东南角。
同一个方格只允许经过一次。但不必做完所有的方格。
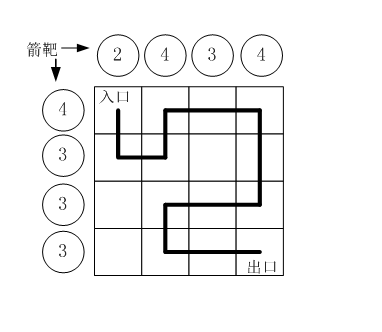
如果只给出靶子上箭的数目,你能推断出骑士的行走路线吗?
有时是可以的,比如图中的例子。
本题的要求就是已知箭靶数字,求骑士的行走路径(测试数据保证路径唯一)
输入:
输出:
为了方便表示,我们约定每个小格子用一个数字代表,从西北角开始编号: 0,1,2,3….
0 1 2 3
样例输入:
样例输出:
资源约定:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 import java.util.Scanner;public class Main { private static int N; private static int [][] direction = { { 0 , 1 }, { 1 , 0 }, { 0 , -1 }, { -1 , 0 } }; private static int [][] oneArray; private static int totalNorth = 0 ; private static int totalWest = 0 ; private static int [] restNorth; private static int [] restWest; private static int [][] visit; private static int [] way = null ; private static int wayLength = 1 ; public static void main (String[] args) { Scanner scanner = new Scanner (System.in); N = scanner.nextInt(); way = new int [N * N + 1 ]; visit = new int [N][N]; oneArray = new int [N][N]; for (int i = 0 , index = 0 ; i < N; i++) for (int j = 0 ; j < N; j++) oneArray[i][j] = index++; restNorth = new int [N]; for (int i = 0 ; i < N; i++) { restNorth[i] = scanner.nextInt(); totalNorth += restNorth[i]; } restWest = new int [N]; for (int i = 0 ; i < N; i++) { restWest[i] = scanner.nextInt(); totalWest += restWest[i]; } scanner.close(); firstStep(); backTrack(0 , 0 ); } private static void firstStep () { restNorth[0 ]--; totalNorth--; restWest[0 ]--; totalWest--; visit[0 ][0 ] = 1 ; way[0 ] = 0 ; } private static void getResult () { for (int i = 0 ; i < wayLength; i++) System.out.print(way[i] + " " ); } public static void backTrack (int x, int y) { if (x == N - 1 && y == N - 1 ) { if (totalNorth == 0 && totalWest == 0 ) { getResult(); } } else { for (int i = 0 ; i < 4 ; i++) { int dx = x + direction[i][0 ]; int dy = y + direction[i][1 ]; if (dx >= 0 && dx < N && dy >= 0 && dy < N && visit[dx][dy] == 0 && restNorth[dy] > 0 && restWest[dx] > 0 ) { visit[dx][dy] = 1 ; restNorth[dy]--; totalNorth--; restWest[dx]--; totalWest--; way[wayLength++] = oneArray[dx][dy]; backTrack(dx, dy); wayLength--; visit[dx][dy] = 0 ; restNorth[dy]++; totalNorth++; restWest[dx]++; totalWest++; } } } } }
碱基 生物学家正在对n个物种进行研究。
现在给定所有生物的DNA序列,请告诉科学家有多少的2m元组是需要关注的。如果两个2m元组有任何一个位置不同,则认为是不同的元组。
输入格式:
输出格式:
样例输入1:
样例输出1:
样例输入2:
样例输出2:
数据规模与约定:
资源约定: