树状数组

树状数组/二叉索引树（Binary Indexed Tree）：

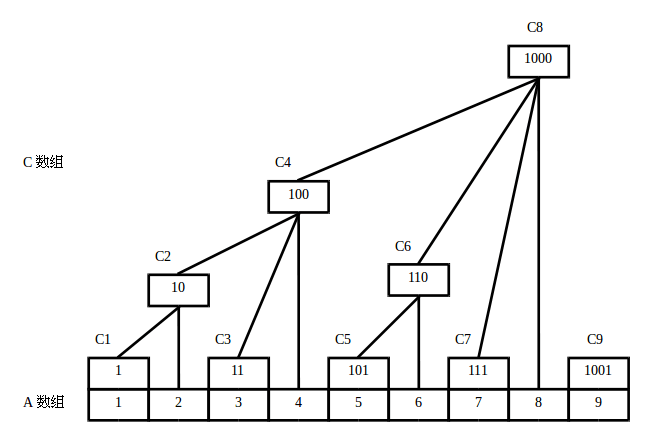
A 数组就是原数组，C 数组则是树状数组。

通过观察可以发现：

[1, 1]  C1 = A1
[1, 2]  C2 = A1 + A2
[3, 3]  C3 = A3
[1, 4]  C4 = A1 + A2 + A3 + A4
[5, 5]  C5 = A5
[5, 6]  C6 = A5 + A6
[7, 7]  C7 = A7
[1, 8]  C8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8

C[i] 管理的区间：[i - bitLow(i) + 1, i]

它的查询和修改的时间复杂度都是 O(logN)，空间复杂度则为 O(N)，这是因为树状数组通过将线性结构转化成树状结构，从而进行跳跃式扫描。

通常使用在高效的计算数列的前缀和，区间和。

模版

class BinaryIndexedTree {
	int length;
	int[] tree;// 数组有效范围 1~length

	/**
	 * 为了统一下标，tree[0]不被使用
	 * 
	 * @param length 数组长度
	 */
	BinaryIndexedTree(int length) {
		this.length = length;
		tree = new int[length + 1];
	}

	/**
	 * index一直加上lowBit(index)，直到index为length
	 * 这些位置的值都加上value
	 * 
	 * @param index 索引
	 * @param value 值
	 */
	void put(int index, int value) {
		while (index <= length) {
			tree[index] += value;
			index += lowBit(index);
		}
	}

	/**
	 * index一直减去lowBit(index)，直到index为length
	 * 这些位置的值都减去value
	 * 
	 * @param index 索引
	 */
	int get(int index) {
		int sum = tree[index];
		int z = index - lowBit(index);
		index--;
		while (index != z) {
			sum -= tree[index];
			index -= lowBit(index);
		}
		return sum;
	}

	/**
	 * 保留k的二进制最低位1的值
	 * 
	 * @param index 索引
	 */
	static int lowBit(int k) {
		// 1110保留最低位1，即最右边1：0010
		return k & -k;
	}

	/**
	 * 计算1~index范围内和
	 * 
	 * @param index 索引
	 */
	int sum(int index) {
		int sum = 0;
		while (index > 0) {
			sum += tree[index];
			index -= lowBit(index);
		}
		return sum;
	}

	/**
	 * 计算start~end范围内和
	 * 
	 * @param start 起始
	 * @param end 终点
	 */
	int sum(int start, int end) {
		return sum(end) - sum(start - 1);
	}
}