二叉搜索树/二叉排序树(Binary Search Tree):
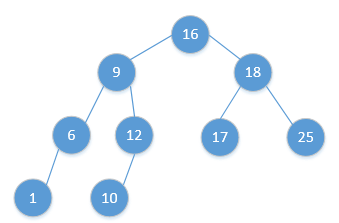
- 根的左子树不空,则左子树上所有结点的值均小于它的根结点的值。
- 根的右子树不空,则右子树上所有结点的值均大于它的根结点的值。
- 根的左、右子树也分别为二叉搜索树。
模版
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
| class BSTree {
class Node {
int key, value;
Node leftChild, rightChild;
Node(int key, int value) {
this.key = key;
this.value = value;
}
}
Node root;
Node query(int key) {
Node currentNode = root;
while (currentNode != null && currentNode.key != key) {
if (key < currentNode.key) {
currentNode = currentNode.leftChild;
} else {
currentNode = currentNode.rightChild;
}
}
return currentNode;
}
void insert(int key, int value) {
if (root == null) {
root = new Node(key, value);
return;
}
Node currentNode = root;
Node parentNode = root;
boolean isLeftChild = true;
while (currentNode != null) {
parentNode = currentNode;
if (key < currentNode.key) {
currentNode = currentNode.leftChild;
isLeftChild = true;
} else {
currentNode = currentNode.rightChild;
isLeftChild = false;
}
}
Node newNode = new Node(key, value);
if (isLeftChild) {
parentNode.leftChild = newNode;
} else {
parentNode.rightChild = newNode;
}
}
boolean delete(int key) {
Node currentNode = root;
Node parentNode = root;
boolean isLeftChild = true;
while (currentNode != null && currentNode.key != key) {
parentNode = currentNode;
if (key < currentNode.key) {
currentNode = currentNode.leftChild;
isLeftChild = true;
} else {
currentNode = currentNode.rightChild;
isLeftChild = false;
}
}
if (currentNode == null) {
return false;
}
if (currentNode.leftChild == null && currentNode.rightChild == null) {
if (currentNode == root) {
root = null;
} else if (isLeftChild) {
parentNode.leftChild = null;
} else {
parentNode.rightChild = null;
}
} else if (currentNode.rightChild == null) {
if (currentNode == root) {
root = currentNode.leftChild;
} else if (isLeftChild) {
parentNode.leftChild = currentNode.leftChild;
} else {
parentNode.rightChild = currentNode.leftChild;
}
} else if (currentNode.leftChild == null) {
if (currentNode == root) {
root = currentNode.rightChild;
} else if (isLeftChild) {
parentNode.leftChild = currentNode.rightChild;
} else {
parentNode.rightChild = currentNode.rightChild;
}
} else {
Node directPostNode = getDirectPostNode(currentNode);
currentNode.key = directPostNode.key;
currentNode.value = directPostNode.value;
}
return true;
}
Node getDirectPostNode(Node delNode) {
Node parentNode = delNode;
Node directPostNode = delNode;
Node currentNode = delNode.rightChild;
while (currentNode != null) {
parentNode = directPostNode;
directPostNode = currentNode;
currentNode = currentNode.leftChild;
}
if (directPostNode != delNode.rightChild) {
parentNode.leftChild = directPostNode.rightChild;
directPostNode.rightChild = null;
}
return directPostNode;
}
void preOrder(Node rootNode) {
if (rootNode != null) {
System.out.println("key: " + rootNode.key + " " + "value: " + rootNode.value);
preOrder(rootNode.leftChild);
preOrder(rootNode.rightChild);
}
}
void inOrder(Node rootNode) {
if (rootNode != null) {
inOrder(rootNode.leftChild);
System.out.println("key: " + rootNode.key + " " + "value: " + rootNode.value);
inOrder(rootNode.rightChild);
}
}
void postOrder(Node rootNode) {
if (rootNode != null) {
postOrder(rootNode.leftChild);
postOrder(rootNode.rightChild);
System.out.println("key: " + rootNode.key + " " + "value: " + rootNode.value);
}
}
}
|

